Home Time Domain Audio 특징 이해와 구현 with librosa
Post
Cancel

Time Domain Audio 특징 이해와 구현 with librosa

Posted Aug 7, 2022 Updated Mar 6, 2023
By Milhaud
5 min read

Time-domain 특징

  • Amplitude envelope (AE)
  • Root-mean-square energy (RMS)
  • Zero-crossing rate (ZCR)

Amplitude envelope (AE)

  • 프레임 내 모든 샘플의 최대 진폭 값
  • 음량에 대한 대략적인 정보 제공
  • Outliers에 민감함
  • Onset detection, 음악 장르 분류

Root-mean-square energy (RMS)

  • 프레임에 있는 모든 표본의 RMS
  • 음량 표시기
  • AE보다 Outliers에 덜 민감함
  • 오디오 세분화, 음악 장르 분류

Zero-crossing rate (ZCR)

  • 타악기 소리와 음조 인식
  • Monophonic pitch 단음 음조 추정
  • 음성 신호에 대한 Voice/unvoiced 결정

1. Basic informations of audio files

Loading the libraries

1
2
3
4
5

import matplotlib.pyplot as plt
import numpy as np
import librosa
import librosa.display
import IPython.display as ipd

Loading audio files

1
2
3

debussy_file = "debussy.wav"
redhot_file = "redhot.wav"
duke_file = "duke.wav"

1

ipd.Audio(debussy_file)

1

ipd.Audio(redhot_file)

1

ipd.Audio(duke_file)

1
2
3
4

# load audio files with librosa
debussy, sr = librosa.load(debussy_file)
redhot, _ = librosa.load(redhot_file)
duke, _ = librosa.load(duke_file)

1

sr

1

22050

Basic information regarding audio files

1

debussy.shape

1

(661500,)

1
2
3

# duration in seconds of 1 sample
sample_duration = 1 / sr
print(f"One sample lasts for {sample_duration:6f} seconds")

1

One sample lasts for 0.000045 seconds

1
2
3

# total number of samples in audio file
tot_samples = len(debussy)
tot_samples

1

661500

1
2
3

# duration of debussy audio in seconds
duration = 1 / sr * tot_samples
print(f"The audio lasts for {duration} seconds")

1

The audio lasts for 30.0 seconds

Visualising audio signal in the time domain

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

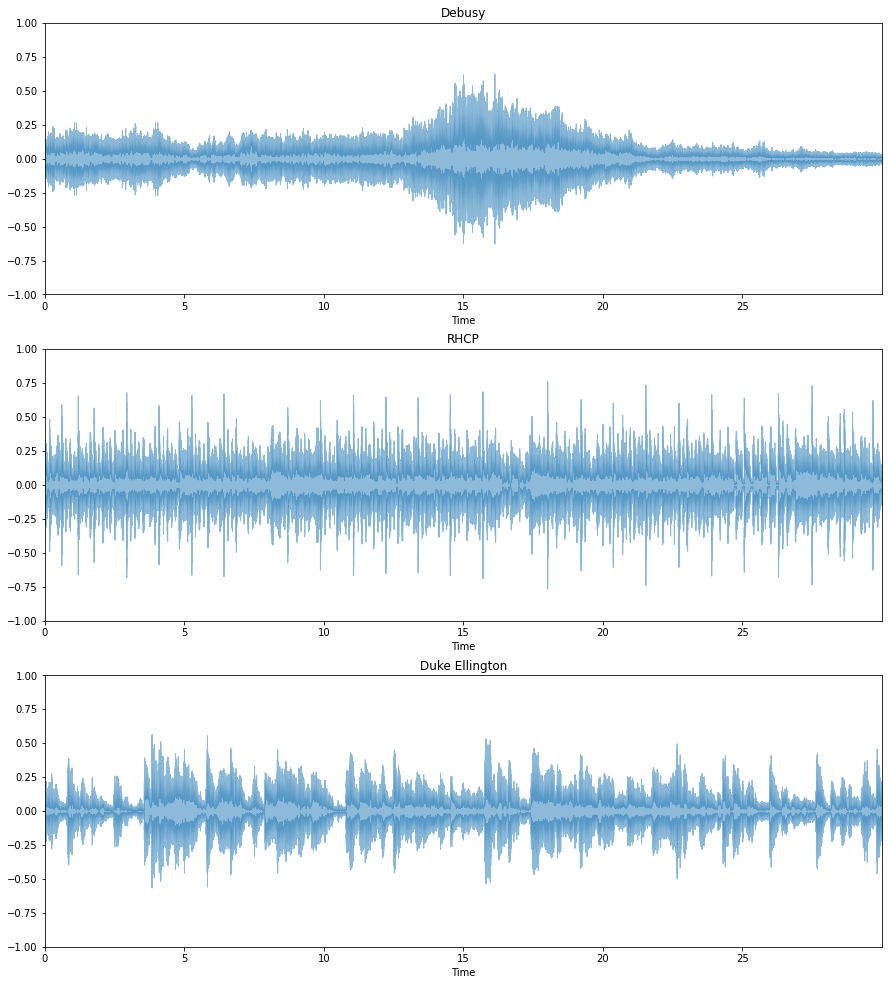
plt.figure(figsize=(15, 17))

plt.subplot(3, 1, 1)
librosa.display.waveplot(debussy, alpha=0.5)
plt.ylim((-1, 1))
plt.title("Debusy")

plt.subplot(3, 1, 2)
librosa.display.waveplot(redhot, alpha=0.5)
plt.ylim((-1, 1))
plt.title("RHCP")

plt.subplot(3, 1, 3)
librosa.display.waveplot(duke, alpha=0.5)
plt.ylim((-1, 1))
plt.title("Duke Ellington")

plt.show()

TimeDomain0

1. Extracting the amplitude envelope feature from scratch

Calculating amplitude envelope

1
2
3
4
5
6
7
8
9
10
11
12
13

FRAME_SIZE = 1024
HOP_LENGTH = 512

def amplitude_envelope(signal, frame_size, hop_length):
    """Calculate the amplitude envelope of a signal with a given frame size nad hop length."""
    amplitude_envelope = []
    
    # calculate amplitude envelope for each frame
    for i in range(0, len(signal), hop_length): 
        amplitude_envelope_current_frame = max(signal[i:i+frame_size]) 
        amplitude_envelope.append(amplitude_envelope_current_frame)
    
    return np.array(amplitude_envelope)

1
2
3

def fancy_amplitude_envelope(signal, frame_size, hop_length):
    """Fancier Python code to calculate the amplitude envelope of a signal with a given frame size."""
    return np.array([max(signal[i:i+frame_size]) for i in range(0, len(signal), hop_length)])

1
2
3

# number of frames in amplitude envelope
ae_debussy = amplitude_envelope(debussy, FRAME_SIZE, HOP_LENGTH)
len(ae_debussy)

1

1292

1
2
3

# calculate amplitude envelope for RHCP and Duke Ellington
ae_redhot = amplitude_envelope(redhot, FRAME_SIZE, HOP_LENGTH)
ae_duke = amplitude_envelope(duke, FRAME_SIZE, HOP_LENGTH)

Visualising amplitude envelope

1
2

frames = range(len(ae_debussy))
t = librosa.frames_to_time(frames, hop_length=HOP_LENGTH)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

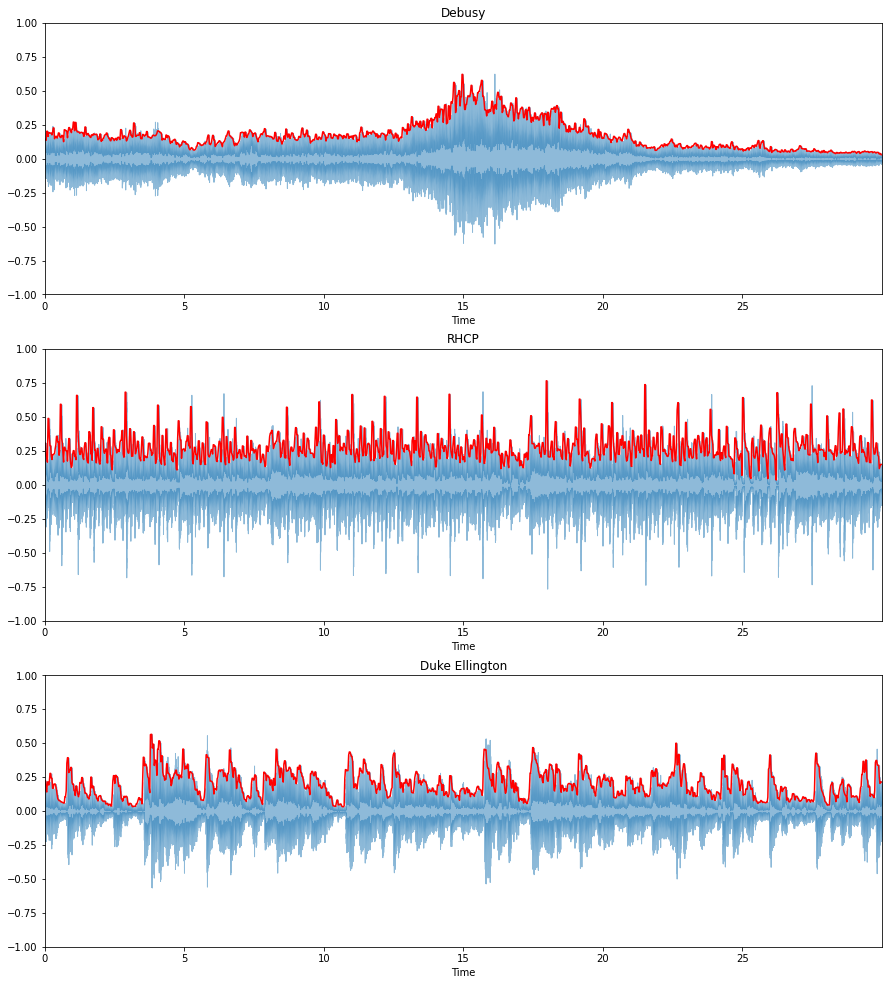
# amplitude envelope is graphed in red

plt.figure(figsize=(15, 17))

ax = plt.subplot(3, 1, 1)
librosa.display.waveplot(debussy, alpha=0.5)
plt.plot(t, ae_debussy, color="r")
plt.ylim((-1, 1))
plt.title("Debusy")

plt.subplot(3, 1, 2)
librosa.display.waveplot(redhot, alpha=0.5)
plt.plot(t, ae_redhot, color="r")
plt.ylim((-1, 1))
plt.title("RHCP")

plt.subplot(3, 1, 3)
librosa.display.waveplot(duke, alpha=0.5)
plt.plot(t, ae_duke, color="r")
plt.ylim((-1, 1))
plt.title("Duke Ellington")

plt.show()

TimeDomain1

2. Extracting Root-Mean Square Energy

Root-mean-squared energy with Librosa

1
2

FRAME_SIZE = 1024
HOP_LENGTH = 512

1
2
3

rms_debussy = librosa.feature.rms(debussy, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]
rms_redhot = librosa.feature.rms(redhot, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]
rms_duke = librosa.feature.rms(duke, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]

Visualise RMSE + waveform

1
2

frames = range(len(rms_debussy))
t = librosa.frames_to_time(frames, hop_length=HOP_LENGTH)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

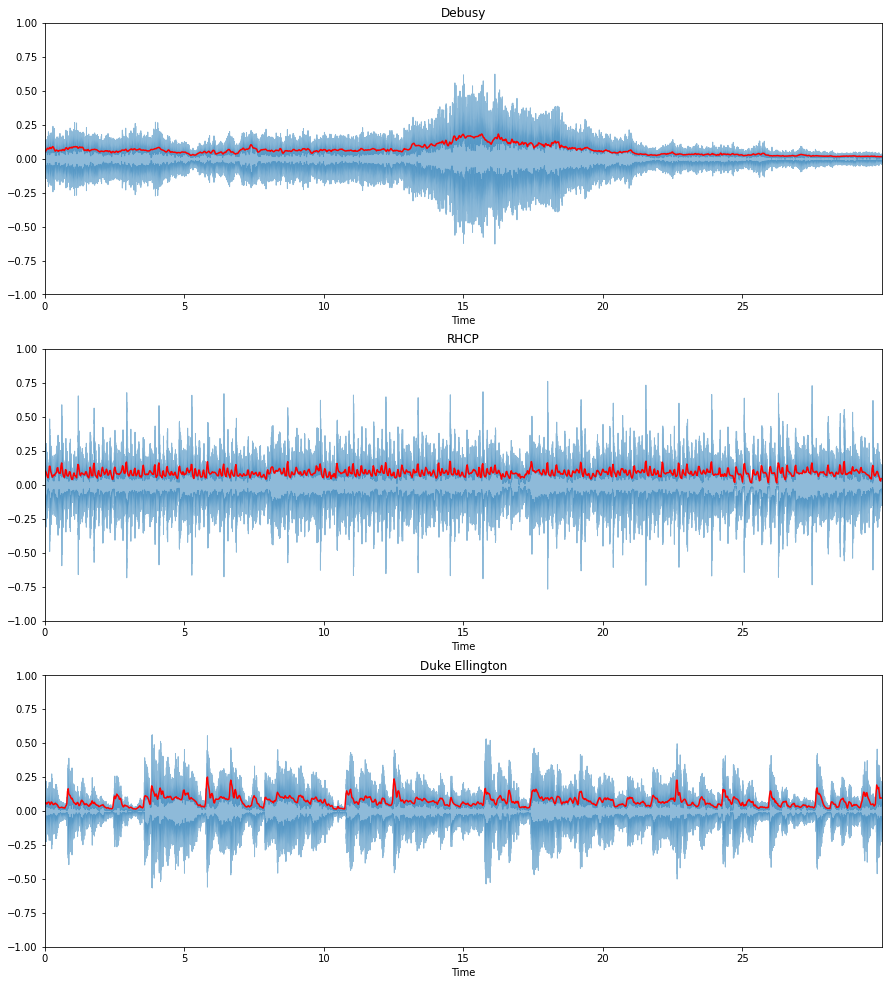
# rms energy is graphed in red

plt.figure(figsize=(15, 17))

ax = plt.subplot(3, 1, 1)
librosa.display.waveplot(debussy, alpha=0.5)
plt.plot(t, rms_debussy, color="r")
plt.ylim((-1, 1))
plt.title("Debusy")

plt.subplot(3, 1, 2)
librosa.display.waveplot(redhot, alpha=0.5)
plt.plot(t, rms_redhot, color="r")
plt.ylim((-1, 1))
plt.title("RHCP")

plt.subplot(3, 1, 3)
librosa.display.waveplot(duke, alpha=0.5)
plt.plot(t, rms_duke, color="r")
plt.ylim((-1, 1))
plt.title("Duke Ellington")

plt.show()

TimeDomain2

RMSE from scratch

1
2
3
4
5
6
7
8

def rmse(signal, frame_size, hop_length):
    rmse = []
    
    # calculate rmse for each frame
    for i in range(0, len(signal), hop_length): 
        rmse_current_frame = np.sqrt(sum(signal[i:i+frame_size]**2) / frame_size)
        rmse.append(rmse_current_frame)
    return np.array(rmse)  

1
2
3

rms_debussy1 = rmse(debussy, FRAME_SIZE, HOP_LENGTH)
rms_redhot1 = rmse(redhot, FRAME_SIZE, HOP_LENGTH)
rms_duke1 = rmse(duke, FRAME_SIZE, HOP_LENGTH)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

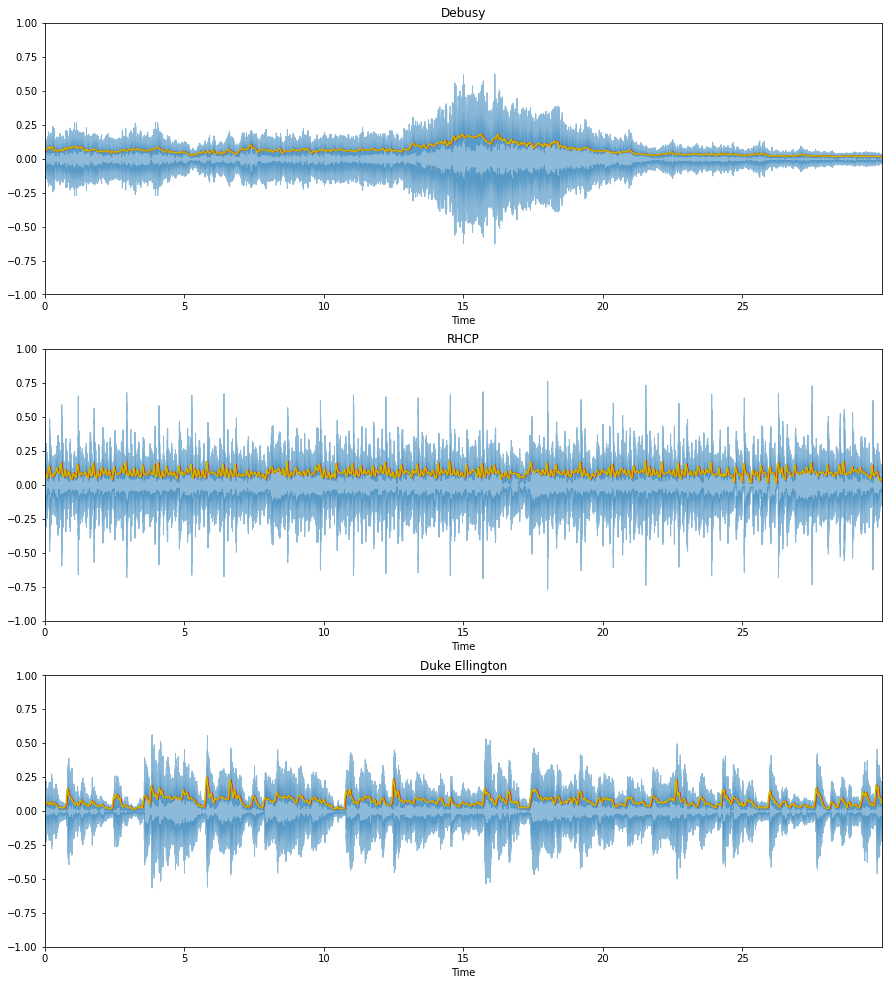
plt.figure(figsize=(15, 17))

ax = plt.subplot(3, 1, 1)
librosa.display.waveplot(debussy, alpha=0.5)
plt.plot(t, rms_debussy, color="r")
plt.plot(t, rms_debussy1, color="y")
plt.ylim((-1, 1))
plt.title("Debusy")

plt.subplot(3, 1, 2)
librosa.display.waveplot(redhot, alpha=0.5)
plt.plot(t, rms_redhot, color="r")
plt.plot(t, rms_redhot1, color="y")
plt.ylim((-1, 1))
plt.title("RHCP")

plt.subplot(3, 1, 3)
librosa.display.waveplot(duke, alpha=0.5)
plt.plot(t, rms_duke, color="r")
plt.plot(t, rms_duke1, color="y")
plt.ylim((-1, 1))
plt.title("Duke Ellington")

plt.show()

TimeDomain3

3. Extracting Zero-Crossing Rate from Audio

Zero-crossing rate with Librosa

1
2
3

zcr_debussy = librosa.feature.zero_crossing_rate(debussy, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]
zcr_redhot = librosa.feature.zero_crossing_rate(redhot, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]
zcr_duke = librosa.feature.zero_crossing_rate(duke, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]

1

zcr_debussy.size

Visualise zero-crossing rate with Librosa

1
2
3
4
5
6
7

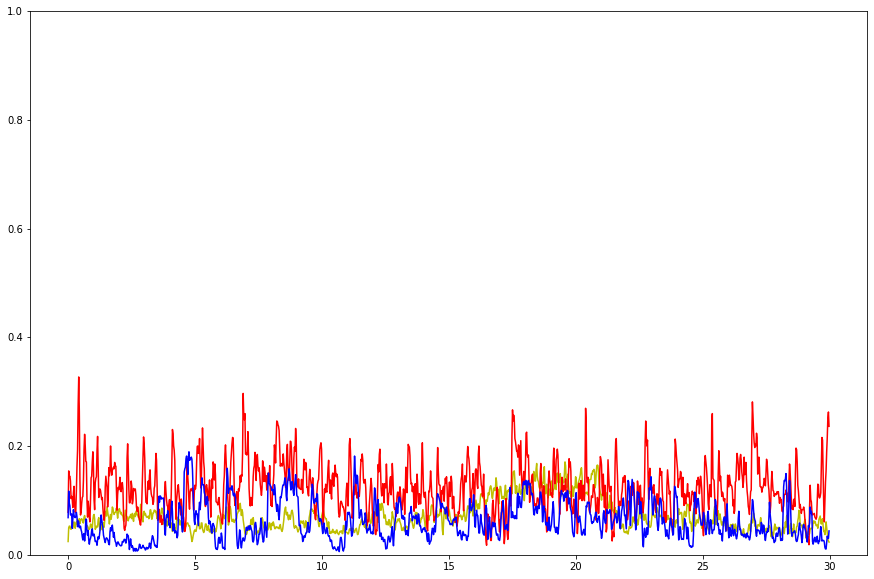
plt.figure(figsize=(15, 10))

plt.plot(t, zcr_debussy, color="y")
plt.plot(t, zcr_redhot, color="r")
plt.plot(t, zcr_duke, color="b")
plt.ylim(0, 1)
plt.show()

TimeDomain4

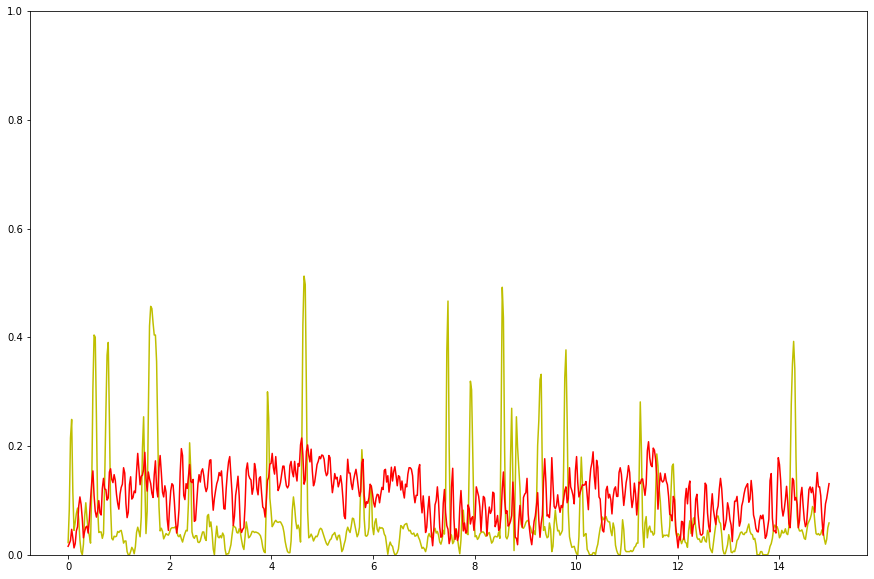
ZCR: Voice vs Noise

1
2

voice_file = "voice.wav"
noise_file = "noise.wav"

1

ipd.Audio(voice_file)

1

ipd.Audio(noise_file)

1
2
3

# load audio files
voice, _ = librosa.load(voice_file, duration=15)
noise, _ = librosa.load(noise_file, duration=15)

1
2
3

# get ZCR
zcr_voice = librosa.feature.zero_crossing_rate(voice, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]
zcr_noise = librosa.feature.zero_crossing_rate(noise, frame_length=FRAME_SIZE, hop_length=HOP_LENGTH)[0]

1
2

frames = range(len(zcr_voice))
t = librosa.frames_to_time(frames, hop_length=HOP_LENGTH)

1
2
3
4
5
6

plt.figure(figsize=(15, 10))

plt.plot(t, zcr_voice, color="y")
plt.plot(t, zcr_noise, color="r")
plt.ylim(0, 1)
plt.show()

TimeDomain5

Reference

Audio Signal Processing
audio signal
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents